割安株を見分けるための指標(INDEX)の紹介もずいぶん続きましたが、まだまだ終わりません。何とかたとえ1銭でも多く儲けたいと思う人がこれまでにさまざまなINDEXを考案してきましたし、その努力は今も続いています。今回は、トレーダーに愛用されている大物INDEX(？)「MACD(マックディー)」です。
MACDは、「Moving Average Convergence – Divergence」の「M」「A」「C」「D」を取った略称で、「移動平均収束拡散法」と訳されます。1979年にジェラルド・アペルによって考案されたINDEX。ジェラルド・アペルは実際に5億ドル超の資産運用を行うトレーダーであり、彼の実績からMACDは世界的に有名で、今なお使用されているINDEXとなっています。
「移動平均収束拡散法」という難しそうな日本語訳となっていますので、この先を読むのも嫌だなぁ、と思うかもしれませんが「だだんだん良くなる法華の太鼓」ですので、面倒くさくとも最後までお付き合いください。MACDは、きっとあなたのトレードに役立ちます。
■MACDの基になるEMA(指数平滑移動平均)、その前に「(単純)移動平均」をおさらい！
さてMACDの基本となっているのは「指数平滑移動平均」です。したがって、まず「指数平滑移動平均」について理解していただきます。
いちいち「指数平滑移動平均」と書いていると長いですし、読むのも面倒でしょうから、ここから「EMA」という略称を用います。
EMAは「Exponential Moving Average」の略で日本語に訳すと「指数平滑移動平均」です。
さて、以前の「乖離(かいりりつ)率」を説明する記事内で「(単純)移動平均」という言葉が出てきましたね。株式銘柄のチャートを見ると、たいていこの「(単純)移動平均」がグラフ線となって表示されています。下のチャートを見てください。
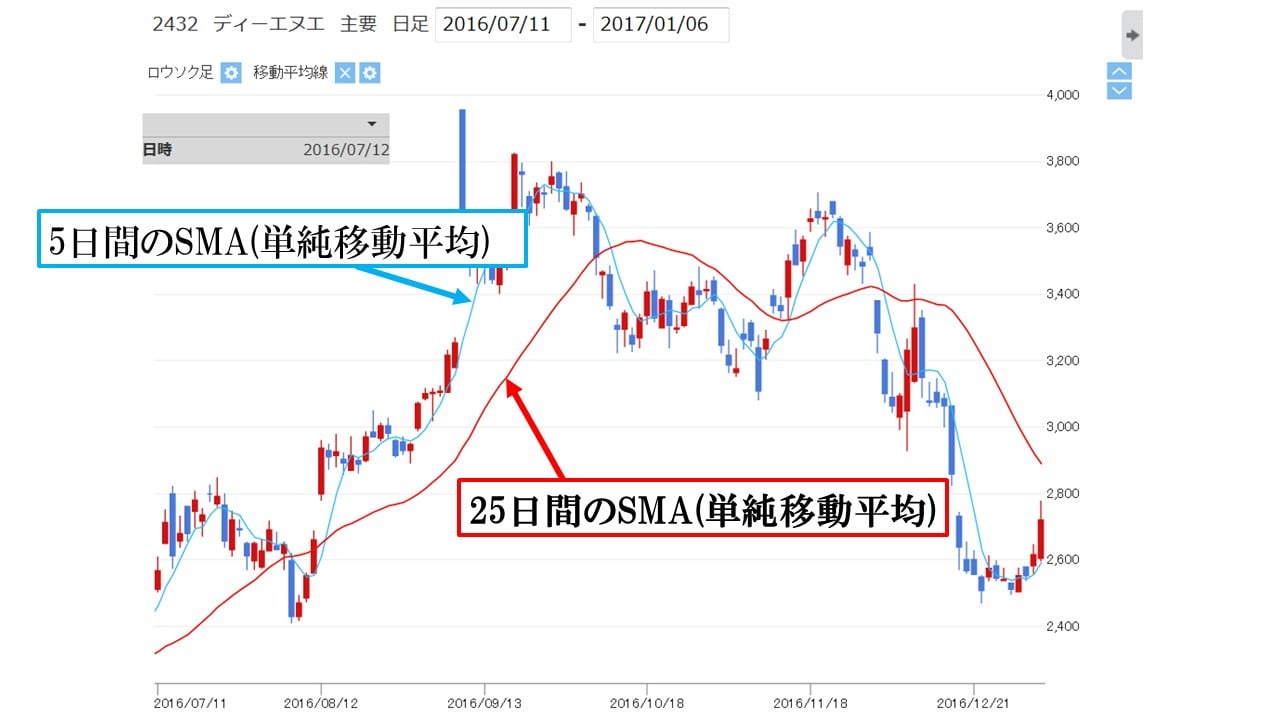
これはディーエヌエー(銘柄：2432)のチャートで、「(単純)移動平均」が水色(5日間)とオレンジ色(25日間)のラインで示されています。「(単純)移動平均」は「Simple Moving Average」の日本語訳で、略称では「SMA」になります。
SMA(単純移動平均)は、直近のある期間内の株価の終値の平均値を示しています。例えば、10日間の(単純)移動平均であれば、「当日の終値、1日前の終値、2日前の終値、3日前の終値……9日前の終値」と直近10日分の終値を足して、これを10(日間)で割ります。
そうすると「その日を含む、直近10日分の終値の平均株価」が当日にプロットできます。これを当日だけでなく、毎日計算するのです。計算された平均株価、チャート上にプロットされた点をつなげるとグラフ線になります。
これがSMA(単純移動平均)のラインです。SMA(単純移動平均)は「5日」「10日」「25日」「75日」などの期間で計算されますが、普通チャート上に表示するのは、短期の株価変動を見る「5日間の単純移動平均線」と、中期の株価変動を見る「25日間の単純移動平均」の2種類のことが多いでしょう。
■SMA(単純移動平均)の弱点は……
SMA(単純移動平均)はデフォルトでチャート上に表示されることが多いので、初心者トレーダーであっても見慣れていますね。SMA(単純移動平均)は分かりやすいINDEXですが、弱点もあるのです。それは、その期間の株価の「単純な平均」であることです。
活発に取り引きが行われ、株価は日々刻々、毎秒毎秒変動しています。ちょっとしたファクターでいかようにも変動します。ですから、30日前の株価よりも直近の株価の方が重要です。この先の株価の変動には、30日前の株価よりも当日の株価の方が大きな影響を与えるでしょう。
SMA(単純移動平均)のラインは、大きな株価の変動を見るには向いているのですが、直近、激しい変動を捉えるには向いていないのです。たとえ直近5日間のSMA(単純移動平均)であっても、5日間の終値の単純平均ですから、当日の大きな変動などはその数字の中に反映させることが難しいのです。またその期間以外の株価は切り捨てられており、あくまでも「5日間」「10日間」といった期間内の平均に過ぎません。
■直近の価格をより重視して移動平均を作ろう！ 「EMA」の登場
そこで、過去の株価の影響は少なくし、直近の株価をより重視して株価の変動を示す「移動平均」が作れないか？ という考えが出てきます。その回答の一つが、MACDの基になる「EMA」(Exponential Moving Averageの略：指数平滑移動平均)なのです。
EMAは、同じ移動平均ですが、SMA(単純移動平均)とは計算方法が大きく違います。面倒くさいかもしれませんが、計算方法をたどってみましょう。
サンプルとして実際のデータを持ってきて、計算してみます。以下はディーエヌエー(銘柄：2432)の2016年11月1日から2017年1月6日までの株価データです。仮にこの日にディーエヌエーが上場され、この日から取り引きが始まったとします。
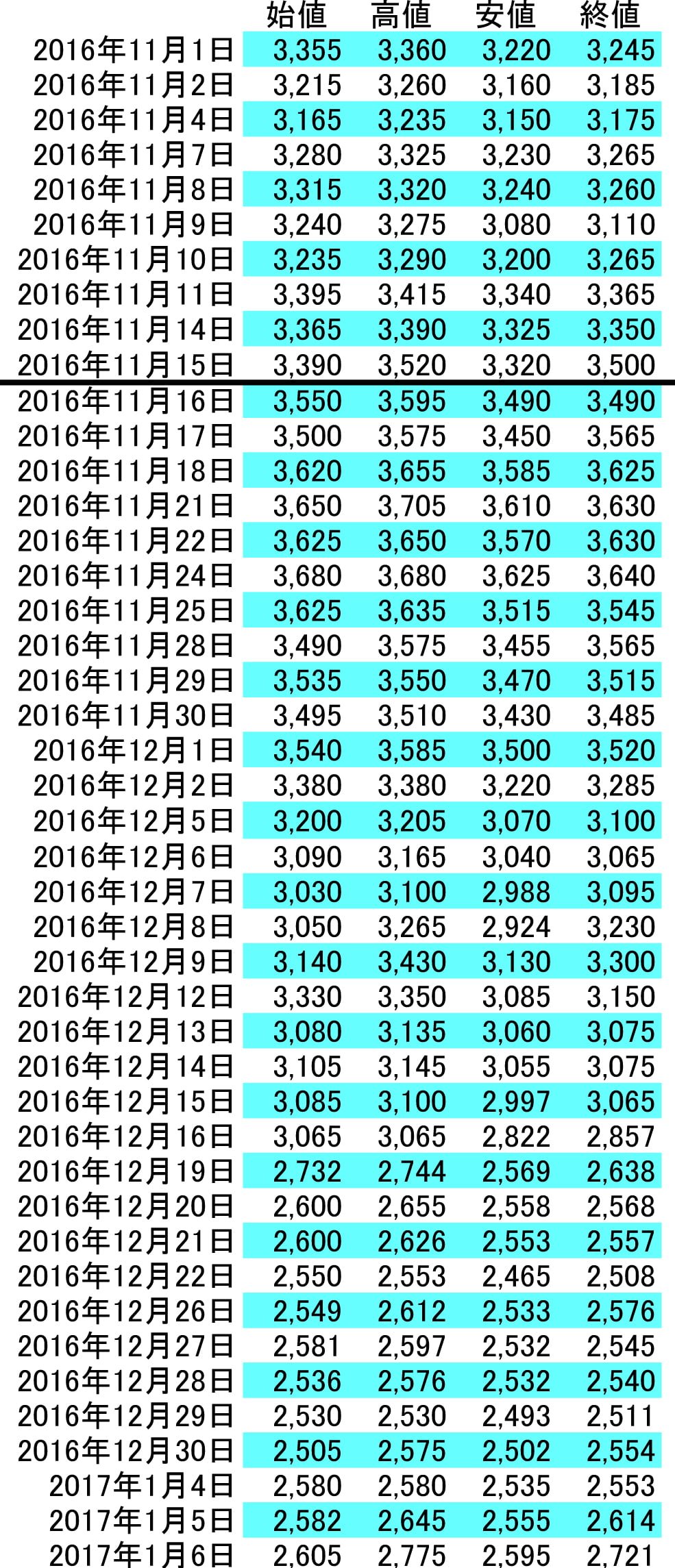これを基に10日間を期間とするEMAを計算してみましょう。
11月1日から11月15日までで「10日間分のデータ」になりますね。11月15日が、10日間のEMA(指数平滑移動平均)を算出できる第1日目です。
最初の日は、それぞれの日の終値の単純平均でOKです。ですからこの例の場合、
11月1日：3,245円
11月2日：3,185円
11月4日：3,175円
11月7日：3,265円
11月8日：3,260円
11月9日：3,110円
11月10日：3,265円
11月11日：3,365円
11月14日：3,350円
11月15日：3,500円
を全部足して、10(日)で割ります。
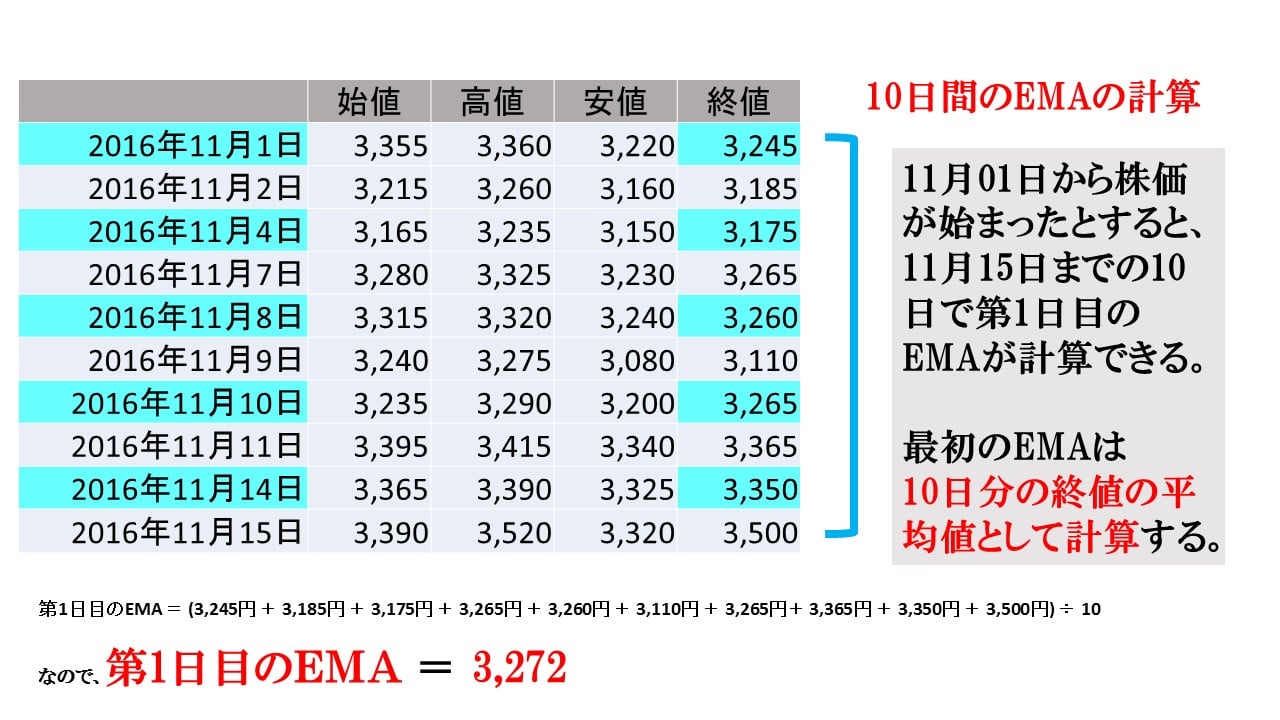EMA ＝ (3,245円 ＋ 3,185円 ＋ 3,175円 ＋ 3,265円 ＋ 3,260円 ＋ 3,110円 ＋ 3,265円＋ 3,365円 ＋ 3,350円 ＋ 3,500円) ÷ 10
ですから、
EMA ＝ 3,272
となります。
第1日目のEMAは「3,272」です。
第2日目のEMA(この場合は11月16日のEMA)は下のようにして計算します。
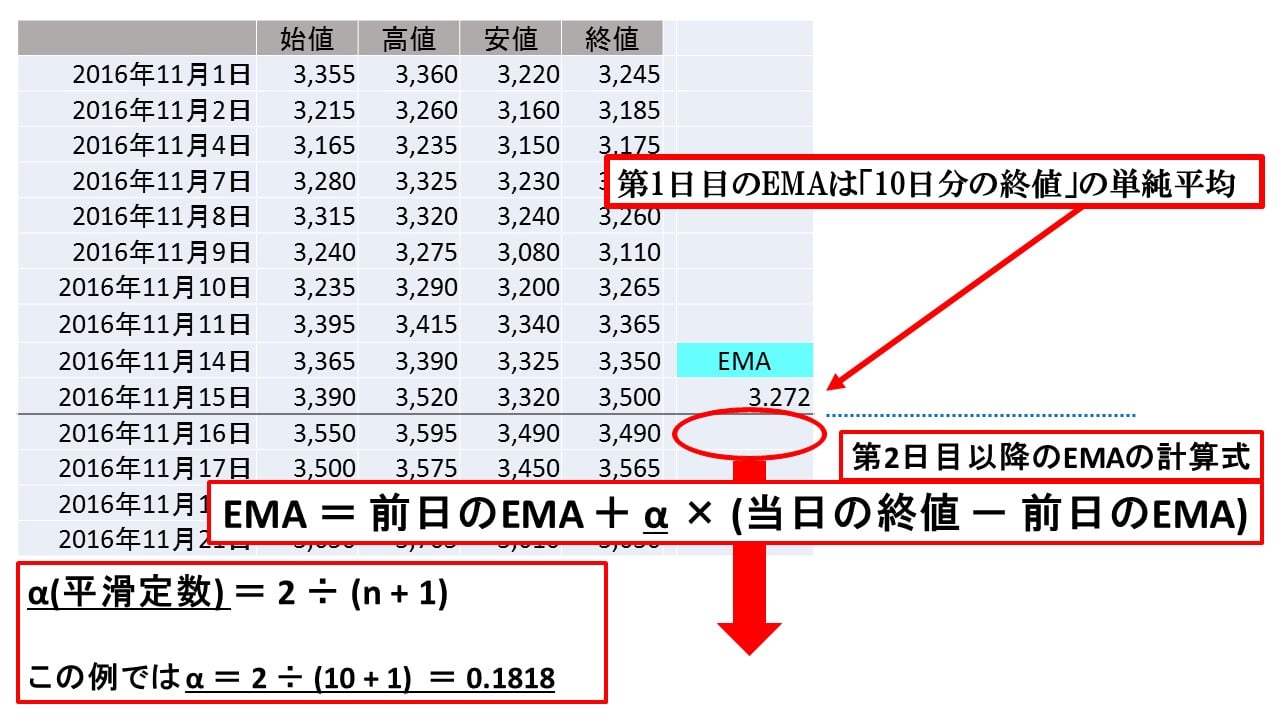
EMA ＝ 前日のEMA ＋ α × (当日の終値 － 前日のEMA)
ここでαという見慣れない記号が出てきます。これは「平滑定数」と呼ばれるもので、次のようにして計算します。
α(平滑定数) ＝ 2 ÷ (n + 1)
nは「○日間」の、○に入る数字です。つまり、「5日間」のEMAを計算するのであれば「5」、「10日間」のEMAを計算するのであれば「10」、「25日間」のEMAを計算するのであれば「25」です。
今回ここで計算しているのは「10日間のEMA」ですので、
α(平滑定数) ＝ 2 ÷ (10 + 1) ＝ 0.1818…
小数点以下第4位まで有効として、とりあえず
α(平滑定数) ＝ 0.1818
としましょう。
この平滑定数を用いて、第2日目(11月16日)のEMAを計算すると、
EMA ＝ 前日のEMA ＋ α × (当日の終値 － 前日のEMA)
なので、
EMA ＝ 3,272 ＋ 0.1818 × (3,490 － 3,272) ＝ 3,311.6363
小数点以下を切り捨てますと「3,311」ですから
11月16日・第2日目のEMAは「3,311」です。
第3日目以降のEMAの計算も、第2日目と同じです。
第3日目・11月17日のEMAも念のためにやってみますと、
EMA ＝ 前日のEMA ＋ α × (当日の終値 － 前日のEMA)
なので
EMA ＝ 3,311 ＋ 0.1818 × (3,565 － 3,311) ＝ 3,357.1817
同様に小数点以下を切り捨てますと「3,357」ですから
11月17日・第3日目のEMAは「3,357」になります。
以下は、第4日目、第5日目……と同様に計算するのです。それぞれの日にEMAがプロットできたらそれを線でつなぎ「EMA(指数平滑移動平均)ライン」に仕上げるわけです。
α(平滑定数)が過去の株価をどの程度株価の変動に取り入れるかを示しています。○日間を示すnを用い、2を「n+1」で割るという式からも分かるとおり、nの数が大きくなればなるほど、分母の数字が大きくなり、平滑定数は小さくなります。つまり、現在から遠い日数の株価ほど影響は小さくなるようにしているわけです。
興味深いのは、当日のEMA(指数平滑移動平均)が前日のEMAを基に計算されるため、過去の株価を断ち切ることなく取り入れていることです。平滑定数「α」に制限されるため、日数がたてばたつほど昔の株価の影響は小さくなるという点が狙いどおりで、SMA(単純移動平均)と違い、株価の連続性を計算するのに巧みな手法だといえるでしょう。
証券会社などの用意しているテクニカル分析ツールでは、普通EMA(指数平滑移動平均)を確認できるようになっています。以下は、筆者が個人的に大変見やすいと思っている『株マップ.com』の「クオンツチャート」による、EMAラインも表示したディーエヌエーのチャートです。
EMA(指数平滑移動平均)は、SMA(単純移動平均)よりも速く売買のサインを出すと説明されます。「MACD」のご紹介の前に、EMA(指数平滑移動平均)の説明だけで大ボリュームになってしまいました。続いて、次回の記事ではEMA(指数平滑移動平均)の特徴について先にご紹介しましょう。
(高橋モータース＠ｄｃｐ)
